#include <Helper.hpp>
Public Types | |
| enum | VarType { Deriv0 = 0 , Deriv1 = 1 } |
| Order of derivative of a function. More... | |
| typedef double | SC |
Static Public Member Functions | |
| static void | computeSurfaceNormal (int dim, vec2D_dbl_ptr_Type pointsRep, vec_int_Type nodeList, vec_dbl_Type &v_E, double &norm_v_E) |
| Compute surface normal of corresponding surface. | |
| static void | buildTransformation (const vec_int_Type &element, vec2D_dbl_ptr_Type pointsRep, SmallMatrix< SC > &B, std::string FEType="P") |
| Build transformation of element to reference element depending on FEType. | |
| static void | buildTransformation (const vec_int_Type &element, vec2D_dbl_ptr_Type pointsRep, SmallMatrix< SC > &B, vec_dbl_Type &b, std::string FEType="P") |
| Build transformation of element to reference element depending on FEType. | |
| static void | buildTransformationSurface (const vec_int_Type &element, vec2D_dbl_ptr_Type pointsRep, SmallMatrix< SC > &B, vec_dbl_Type &b, std::string FEType="P") |
| Transformation of a surface to the reference element. | |
| static void | gradPhi (int Dimension, int intFE, int i, vec_dbl_Type &QuadPts, vec_dbl_ptr_Type &value) |
| Returning gradient of phi evaluated at the quadrature points. | |
| static void | getQuadratureValues (int Dimension, int Degree, vec2D_dbl_ptr_Type &QuadPts, vec_dbl_ptr_Type &QuadW, std::string FEType) |
| Get quadrature formula. | |
| static vec2D_dbl_Type | getQuadratureValuesOnSurface (int dim, std::string FEType, vec_dbl_Type &QuadW, vec_LO_Type surfaceIDs, vec2D_dbl_ptr_Type points) |
| Returns quadrature formula on surface element. | |
| static int | getDPhi (vec3D_dbl_ptr_Type &DPhi, vec_dbl_ptr_Type &weightsDPhi, int Dimension, std::string FEType, int Degree) |
| Full matrix representation of gradient of a basis function for each quadrature point. | |
| static void | getDPhiAtCM (vec3D_dbl_ptr_Type &DPhi, int dim, std::string FEType) |
| static void | applyBTinv (vec3D_dbl_ptr_Type &dPhiIn, vec3D_dbl_Type &dPhiOut, const SmallMatrix< SC > &Binv) |
| Applying the transformation matriX B to the gradient of phi, as is done in when transforming the gradient of phi to the reference element. | |
| static UN | determineDegree (UN dim, std::string FEType, VarType orderOfDerivative) |
| Determine polynomial degree of a finite element basis function or its gradient that is required to select the correct quadrature formula for exact integration. | |
| static int | getPhi (vec2D_dbl_ptr_Type &Phi, vec_dbl_ptr_Type &weightsPhi, int dim, std::string FEType, int Degree, std::string FETypeQuadPoints="") |
| Get basisfunction phi per quadrature point. | |
| static int | getFuncAtQuadNodes (vec_dbl_ptr_Type &funcVals, RhsFunc_Type &rhsFunc, int dim, std::string FEType, int Degree, std::string FETypeQuadPoints="") |
| static void | phi (int dim, int intFE, int i, vec_dbl_Type &p, double *value) |
| Get phi i. | |
Detailed Description
Helper class of static functions that contains rudimental finite element components. It contains basis functions, quadrature rules, transformation functions, and other stuff.
Member Enumeration Documentation
◆ VarType
Member Function Documentation
◆ applyBTinv()
|
static |
Applying the transformation matriX B to the gradient of phi, as is done in when transforming the gradient of phi to the reference element.
- Parameters
-
dPhiIn dPhiOut Binv
◆ buildTransformation() [1/2]
|
static |
Build transformation of element to reference element depending on FEType.
- Parameters
-
[in] element Finite element [in] pointsRep List of repeated points [out] B Resulting transformation matrix [in] FEType FE Discretization
◆ buildTransformation() [2/2]
|
static |
Build transformation of element to reference element depending on FEType.
- Parameters
-
[in] element Finite element [in] pointsRep List of repeated points [out] B Resulting transformation matrix [in] b Point to transform from [in] FEType FE Discretization
◆ buildTransformationSurface()
|
static |
Transformation of a surface to the reference element.
- Parameters
-
[in] element Finite element [in] pointsRep List of repeated points [out] B Resulting transformation matrix [in] b Point to transform from [in] FEType FE Discretization
◆ computeSurfaceNormal()
|
static |
Compute surface normal of corresponding surface.
- Parameters
-
[in] dim Dimension [in] pointsRep List of all repeated nodes [in] nodeList Ids of local surface points [out] v_E normal vector [out] norm_v_E Normal vector length
◆ determineDegree()
|
static |
Determine polynomial degree of a finite element basis function or its gradient that is required to select the correct quadrature formula for exact integration.
This is a wrapper. See Helper::requiredQuadratureDegreeForBasisfunction for details in case the degree is required for a basis function. See Helper::requiredQuadratureDegreeForGradientOfBasisfunction for details in case the degree is required for the gradient of a basis function.
- Parameters
-
[in] dim Dimension of the domain. [in] FEType Finite element type, e.g., "P1", "Q2" etc. [in] orderOfDerivative {Deriv0,Deriv1} Order of the derivative: order=0 (type=Deriv0) is the original function, order=1 (type=Deriv1) is the gradient, i.e., the first derivative.
- Returns
- a polynomial degree for a finite element basis function or its gradient
◆ getDPhi()
|
static |
Full matrix representation of gradient of a basis function for each quadrature point.
- Parameters
-
DPhi grad Phi per quadpoint dim:(quadpoint,i,j) weightsDPhi Quadrature weights Dimension Dimension FEType Finite Element Type Degree Integration degree
- Returns
◆ getDPhiAtCM()
|
static |
- Parameters
-
DPhi grad Phi p Dimension Dimension FEType Finite Element Type


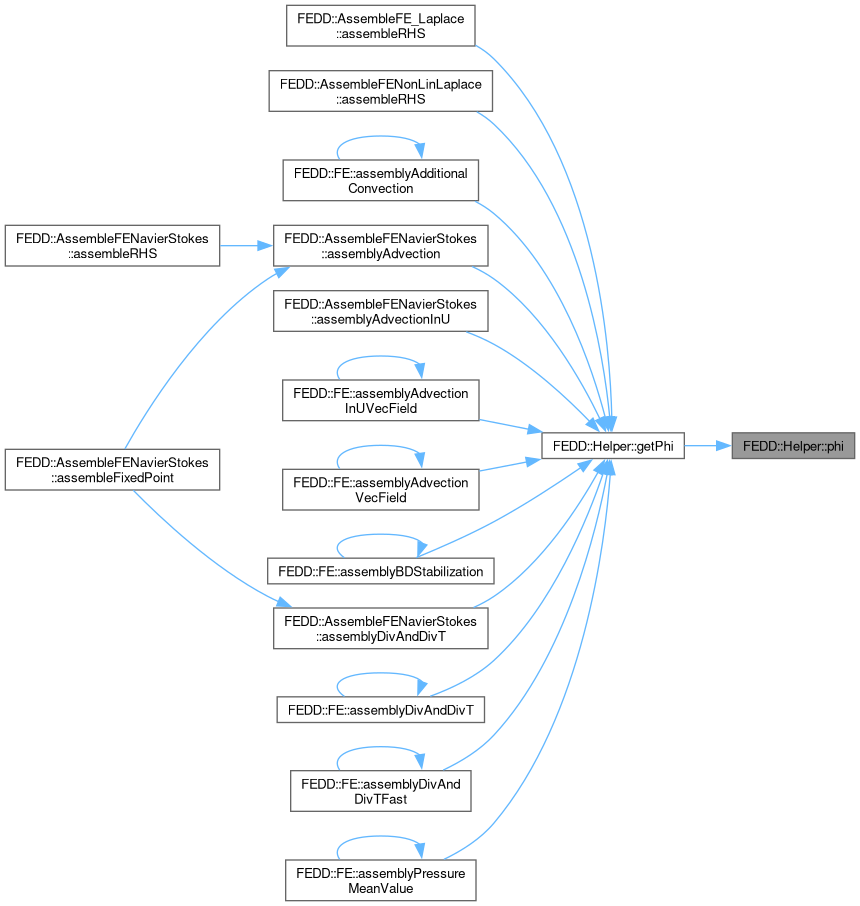
◆ getPhi()
|
static |
Get basisfunction phi per quadrature point.
- Parameters
-
Phi Basisfunction phi per quad point with (quadpoint,i) weightsPhi Quadrature weights dim dimension FEType Finite element discretization Degree Integration degree FETypeQuadPoints
- Returns
◆ getQuadratureValues()
|
static |
Get quadrature formula.
A quadrature formula is used to integrate approximate an integral of f(x) over the domain Omega, i.e., integral_Omega f(x) dx, via the following sum: sum_i f(xi)*wi, where xi is a quadrature point, and wi a quadrature weight.
Source of the formulas: Most of the quadrature formulas can be found in http://code-aster.org/doc/v11/en/man_r/r3/r3.01.01.pdf 01/2021
- Parameters
-
[in] Dimension Space dimension d of the domain of f:IR^d-->IR. [in] Degree Order of polynomial that must be integrated exactly in exact arithmetic with the returned formula. [out] QuadPts Quadrature points [out] QuadW Quadrature weights [in] FEType Finite element type, e.g., "P1", "Q2" etc.
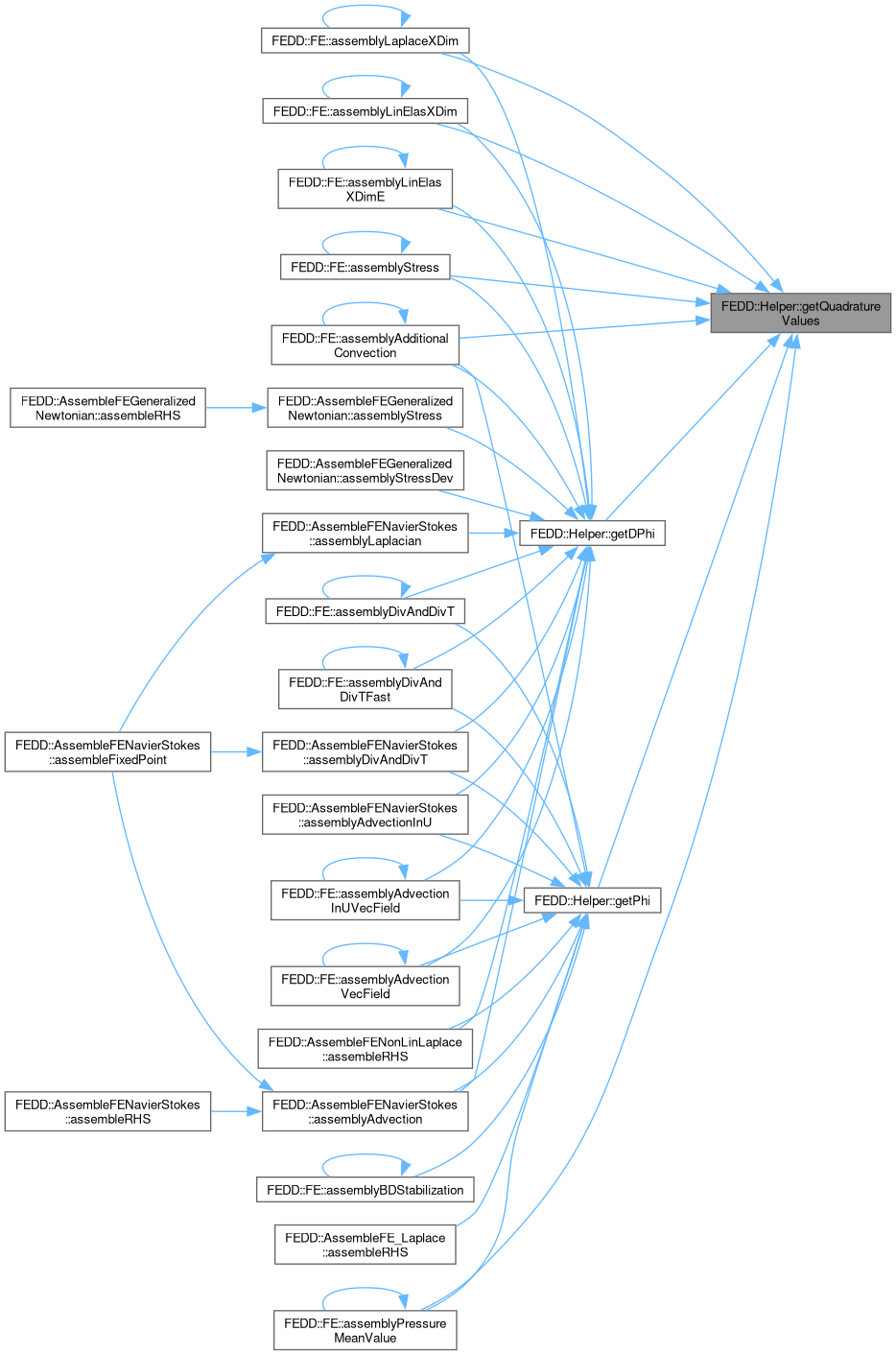
◆ getQuadratureValuesOnSurface()
|
static |
Returns quadrature formula on surface element.
Is distinguishes between needing Element or Surface information. !! Input can be improved with just delivering the coordinates of the surface nodes to determine the quad points
Keep in mind that elementwise quadPoints are defined on reference element whereas surface quadPoints at hand are defined on the input surface, which is typically not the reference Element.
- Parameters
-
[in] dim Space dimension of the underlying domain, e.g., 3 for a triangle in IR^3.. [in] FEType Finite element type of the underlying element (P1, P2, Q1 etc.), e.g., a "P2" tetrahedron for which a quadrature formula on one of its surface elements (triangles) is required. [out] QuadW Vector to be filled with the quadrature weights [in] vec_LO_Type surfaceIDs for which you need the quadrature points. [in] points The repeated(!) points of current problem to identify the surface node ids.
- Returns
- Quadrature points
◆ gradPhi()
|
static |
Returning gradient of phi evaluated at the quadrature points.
- Parameters
-
[in] Dimension Dimension [in] intFE number corresponding to FE disc. [in] i basisfunction i [in] QuadPts quadpoints [out] value vector including values

◆ phi()
|
static |
Get phi i.
- Parameters
-
dim intFE i p value
The documentation for this class was generated from the following files:
- feddlib/core/FE/Helper.hpp
- feddlib/core/FE/Helper.cpp