Public Types
typedef Mesh< SC, LO, GO, NO >	Mesh_Type

typedef MeshUnstructured< SC, LO, GO, NO >	MeshUnstr_Type

typedef Teuchos::RCP< MeshUnstructured< SC, LO, GO, NO > >	MeshUnstrPtr_Type

typedef std::vector< MeshUnstrPtr_Type >	MeshUnstrPtrArray_Type

typedef Mesh_Type::CommPtr_Type	CommPtr_Type

typedef Mesh_Type::CommConstPtr_Type	CommConstPtr_Type

typedef Elements	Elements_Type

typedef Teuchos::RCP< Elements_Type >	ElementsPtr_Type

typedef SurfaceElements	SurfaceElements_Type

typedef Teuchos::RCP< SurfaceElements_Type >	SurfaceElementsPtr_Type

typedef EdgeElements	EdgeElements_Type

typedef Teuchos::RCP< EdgeElements_Type >	EdgeElementsPtr_Type

typedef Map< LO, GO, NO >	Map_Type

typedef Map_Type::MapPtr_Type	MapPtr_Type

typedef Map_Type::MapConstPtr_Type	MapConstPtr_Type

typedef MultiVector< SC, LO, GO, NO >	MultiVector_Type

typedef Teuchos::RCP< MultiVector_Type >	MultiVectorPtr_Type

typedef MultiVector< LO, LO, GO, NO >	MultiVectorLO_Type

typedef Teuchos::RCP< MultiVectorLO_Type >	MultiVectorLOPtr_Type

typedef MultiVector< GO, LO, GO, NO >	MultiVectorGO_Type

typedef Teuchos::RCP< MultiVectorGO_Type >	MultiVectorGOPtr_Type

typedef Teuchos::RCP< const MultiVector_Type >	MultiVectorConstPtr_Type

typedef Teuchos::OrdinalTraits< LO >	OTLO

typedef Matrix< SC, LO, GO, NO >	Matrix_Type

typedef Teuchos::RCP< Matrix_Type >	MatrixPtr_Type

typedef ExporterParaViewAMR< SC, LO, GO, NO >	Exporter_Type

typedef Teuchos::RCP< Exporter_Type >	ExporterPtr_Type

typedef Teuchos::RCP< ExporterTxt >	ExporterTxtPtr_Type

typedef Problem< SC, LO, GO, NO >	Problem_Type

typedef Teuchos::RCP< Problem_Type >	ProblemPtr_Type

typedef Domain< SC, LO, GO, NO >	Domain_Type

typedef Teuchos::RCP< Domain_Type >	DomainPtr_Type

typedef std::vector< DomainPtr_Type >	DomainPtrArray_Type

typedef std::vector< MultiVectorPtr_Type >	MultiVectorPtrArray_Type

typedef BlockMultiVector< SC, LO, GO, NO >	BlockMultiVector_Type

typedef Teuchos::RCP< BlockMultiVector_Type >	BlockMultiVectorPtr_Type

typedef Teuchos::RCP< const BlockMultiVector_Type >	BlockMultiVectorConstPtr_Type

Public Member Functions
	AdaptiveMeshRefinement (ParameterListPtr_Type parameterListAll)
	Initializing mesh refinement with minimal information. This is only useful for refining either uniformaly or only a certain area.

	AdaptiveMeshRefinement (std::string problemType, ParameterListPtr_Type parameterListAll)
	Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType). This constructor is used if no exact solutions are known.

	AdaptiveMeshRefinement (std::string problemType, ParameterListPtr_Type parameterListAll, Func_Type exactSolFunc)
	Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType).

	AdaptiveMeshRefinement (std::string problemType, ParameterListPtr_Type parameterListAll, Func_Type exactSolFuncU, Func_Type exactSolFuncP)
	Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType).

DomainPtr_Type	globalAlgorithm (DomainPtr_Type domainP1, DomainPtr_Type domainP12, BlockMultiVectorConstPtr_Type solution, ProblemPtr_Type problem, RhsFunc_Type rhsFunc)
	Global Algorithm of Mesh Refinement.

DomainPtr_Type	refineArea (DomainPtr_Type domainP1, vec2D_dbl_Type area, int level)
	Initializing problem if only a certain area should be refined.

DomainPtr_Type	refineUniform (DomainPtr_Type domainP1, int level)
	Initializing problem if uniform refinement is requested.

DomainPtr_Type	refineFlag (DomainPtr_Type domainP1, int level, int flag)

MultiVectorConstPtr_Type	calcExactSolution ()
	Calculating exact solution for velocity if possible with exactSolFunc_.

MultiVectorConstPtr_Type	calcExactSolutionP ()
	Calculating exact solution for pressure if possible with exactSolPFunc_.

void	identifyProblem (BlockMultiVectorConstPtr_Type valuesSolution)
	Identifying the problem with respect to the degrees of freedom and whether we calculate pressure. By telling how many blocks the MultiVector has, we can tell whether we calculate pressure or not. Depending on the numbers of entries within the solution vector, we can tell how many degreesOfFreedom (dofs) we have.

void	calcErrorNorms (MultiVectorConstPtr_Type exactSolution, MultiVectorConstPtr_Type solutionP12, MultiVectorConstPtr_Type exactSolutionP)
	Calculating error norms. If the exact solution is unknown we use approxmated error norm and error indicators.

void	initExporter (ParameterListPtr_Type parameterListAll)
	ParaViewExporter initiation. ParameterListAll contains most settings for ExporterParaView. ExporterParaViewAMR is an extension of ExportParaView and as such uses its setup.

void	exportSolution (MeshUnstrPtr_Type mesh, MultiVectorConstPtr_Type exportSolutionMv, MultiVectorConstPtr_Type errorValues, MultiVectorConstPtr_Type exactSolutionMv, MultiVectorConstPtr_Type exportSolutionPMv, MultiVectorConstPtr_Type exactSolutionPMv)
	ParaViewExporter export of solutions and other error values on current mesh.

void	exportError (MeshUnstrPtr_Type mesh, MultiVectorConstPtr_Type errorElConst, MultiVectorConstPtr_Type errorElConstH1, MultiVectorConstPtr_Type difH1Eta, MultiVectorConstPtr_Type vecDecompositionConst)
	ParaViewExporter export of solutions and other error values on current mesh.

void	writeRefinementInfo ()
	Writing refinement information at the end of mesh refinement.

void	buildSurfaceTriangleElements (ElementsPtr_Type elements, EdgeElementsPtr_Type edgeElements, SurfaceElementsPtr_Type surfaceTriangleElements)

vec_bool_Type	checkInterfaceSurface (EdgeElementsPtr_Type edgeElements, vec_int_Type originFlag, vec_int_Type edgeNumbers, int indexElement)

Constructor & Destructor Documentation

◆ AdaptiveMeshRefinement() [1/4]

template<class SC, class LO, class GO, class NO>

FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::AdaptiveMeshRefinement ( ParameterListPtr_Type parameterListAll )

Initializing mesh refinement with minimal information. This is only useful for refining either uniformaly or only a certain area.

Parameters

[in] int dim

◆ AdaptiveMeshRefinement() [2/4]

template<class SC, class LO, class GO, class NO>

FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::AdaptiveMeshRefinement	(	std::string	problemType,
		ParameterListPtr_Type	parameterListAll )

Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType). This constructor is used if no exact solutions are known.

Parameters

[in]	problemType	Laplace, Stokes, NavierStokes.
[in]	parameterListAll	Parameterlist as used as input parametersProblem.xml.

◆ AdaptiveMeshRefinement() [3/4]

template<class SC, class LO, class GO, class NO>

FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::AdaptiveMeshRefinement	(	std::string	problemType,
		ParameterListPtr_Type	parameterListAll,
		Func_Type	exactSolFunc )

Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType).

Parameters

[in]	problemType	Laplace, Stokes, NavierStokes.
[in]	paramerterListAll	Parameterlist as used as input parametersProblem.xml.
[in]	exactSolFun	Exact solution function.

◆ AdaptiveMeshRefinement() [4/4]

template<class SC, class LO, class GO, class NO>

FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::AdaptiveMeshRefinement	(	std::string	problemType,
		ParameterListPtr_Type	parameterListAll,
		Func_Type	exactSolFuncU,
		Func_Type	exactSolFuncP )

Initializing problem with the kind of problem we are solving for determining the correct error estimation. ParameterListAll delivers all necessary information (i.e. dim, feType).

Parameters

[in]	problemType	Laplace, Stokes, NavierStokes.
[in]	paramerterListAll	Parameterlist as used as input parametersProblem.xml.
[in]	exactSolFunU	Exact solution for velocity u.
[in]	exactSolFunP	Exact solution for velocity p.

Member Function Documentation

◆ calcErrorNorms()

template<class SC, class LO, class GO, class NO>

void FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::calcErrorNorms	(	MultiVectorConstPtr_Type	exactSolution,
		MultiVectorConstPtr_Type	solutionP12,
		MultiVectorConstPtr_Type	exactSolutionP )

Calculating error norms. If the exact solution is unknown we use approxmated error norm and error indicators.

Parameters

[in]	exactSolution	If known, otherwise a dummy vector with all zeros is input.
[in]	solutionP12	Finite element solution u_h and maybe p_h.
[in]	exactSolutionP	If known, otherwise a vector with all zeros is input.

Here is the caller graph for this function:

◆ exportError()

template<class SC, class LO, class GO, class NO>

void FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::exportError	(	MeshUnstrPtr_Type	mesh,
		MultiVectorConstPtr_Type	errorElConst,
		MultiVectorConstPtr_Type	errorElConstH1,
		MultiVectorConstPtr_Type	difH1Eta,
		MultiVectorConstPtr_Type	vecDecompositionConst )

ParaViewExporter export of solutions and other error values on current mesh.

Parameters

[in]	mesh	The current mesh on which refinement is performed.
[in]	errorElConst	Estimated error eta_T.
[in]	errorElConstH1	H1 error elmentwise.
[in]	difH1Eta	\|eta_T-\|\nabla u_h\|_T\| difference between estimated error an H1-error.
[in]	vecDecompositionConst	Information of distribution of elements among processors.

Here is the caller graph for this function:

◆ exportSolution()

template<class SC, class LO, class GO, class NO>

void FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::exportSolution	(	MeshUnstrPtr_Type	mesh,
		MultiVectorConstPtr_Type	exportSolutionMv,
		MultiVectorConstPtr_Type	errorValues,
		MultiVectorConstPtr_Type	exactSolutionMv,
		MultiVectorConstPtr_Type	exportSolutionPMv,
		MultiVectorConstPtr_Type	exactSolutionPMv )

ParaViewExporter export of solutions and other error values on current mesh.

Parameters

[in]	mesh	The current mesh on which refinement is performed.
[in]	exportSolutionMv	Export vector of velocity fe solution.
[in]	exportSolutionPMv	Export vector of pressure fe solution.
[in]	errorValue	\|u-u_h\| on domainP12.
[in]	exactSolutionMv	Export vector of exact velocity solution.
[in]	exactSolutionPMv	Export vector of exact pressure solution.

Here is the caller graph for this function:

◆ globalAlgorithm()

template<class SC, class LO, class GO, class NO>

AdaptiveMeshRefinement< SC, LO, GO, NO >::DomainPtr_Type FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::globalAlgorithm	(	DomainPtr_Type	domainP1,
		DomainPtr_Type	domainP12,
		BlockMultiVectorConstPtr_Type	solution,
		ProblemPtr_Type	problem,
		RhsFunc_Type	rhsFunc )

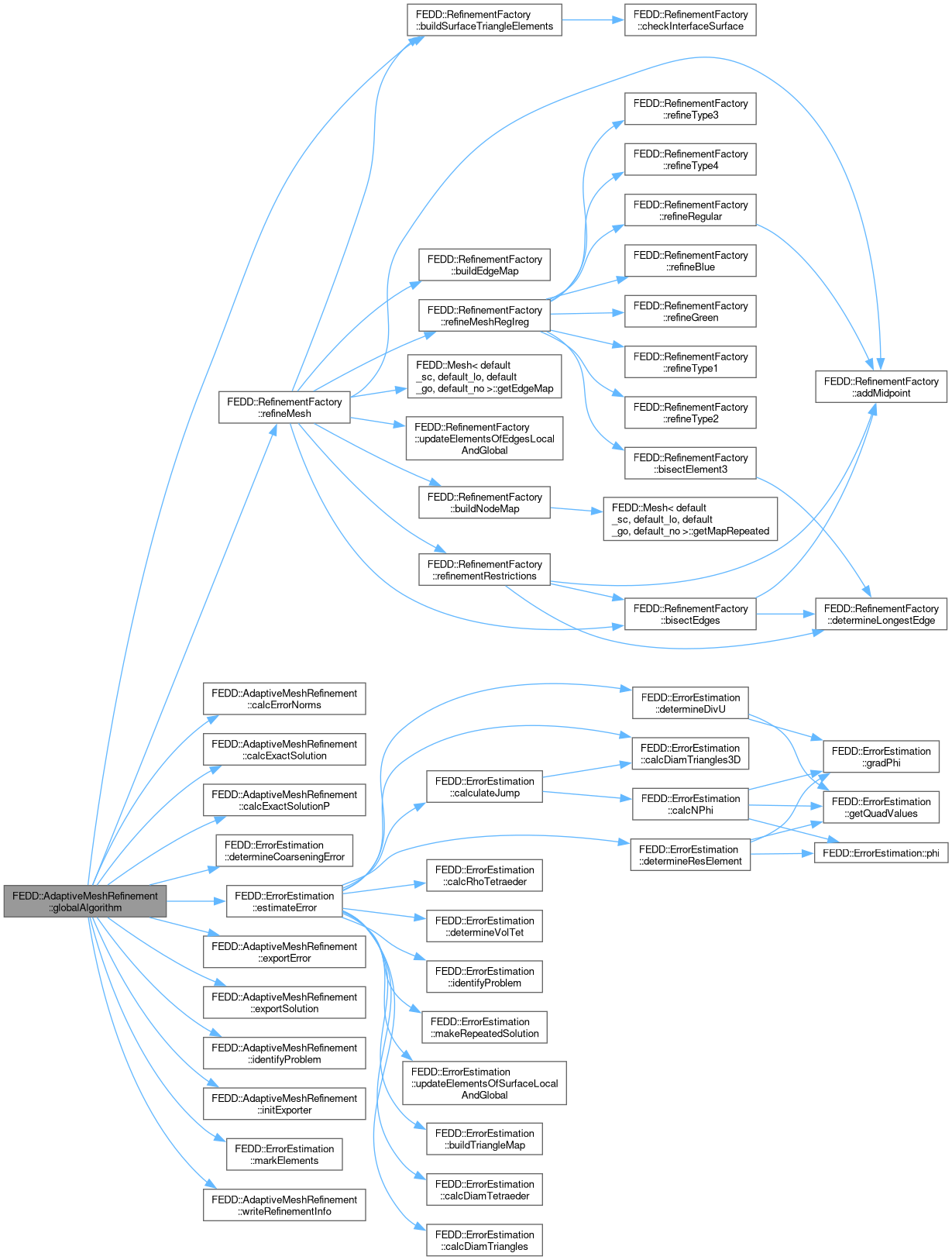
Global Algorithm of Mesh Refinement.

Given domains and solutions depending on problem a global mesh refinement algorithm and error estimation is performed. For example if to solve simple laplace problem, we have only one solution to put in, if to estimate error for Navier-Stokes equation we need pressure and velocity solutions.

Parameters

[in]	domainP1	Domain with P_1 discretization, always neccesary as refinement is performed on P_1 mesh.
[in]	domainP12	Domain with P_1 or P_2 discretization if available, otherwise input domainP1.
[in]	solution	Solution of problem on P_1 or P_2 discretization, can contain velocity and pressure solution.
[in]	problem	The problem itself as the problemPtr. Contains Laplace, Stokes or Navier-Stokes problem.
[in]	rhs	Right hand side function from the pde system. Necessary for error estimation.

Here is the call graph for this function:

◆ identifyProblem()

template<class SC, class LO, class GO, class NO>

void FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::identifyProblem ( BlockMultiVectorConstPtr_Type valuesSolution )

Identifying the problem with respect to the degrees of freedom and whether we calculate pressure. By telling how many blocks the MultiVector has, we can tell whether we calculate pressure or not. Depending on the numbers of entries within the solution vector, we can tell how many degreesOfFreedom (dofs) we have.

Parameters

[in] valuesSolution Block that contains solution for velocity and as the case may be pressure.

Here is the caller graph for this function:

◆ refineArea()

template<class SC, class LO, class GO, class NO>

AdaptiveMeshRefinement< SC, LO, GO, NO >::DomainPtr_Type FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::refineArea	(	DomainPtr_Type	domainP1,
		vec2D_dbl_Type	area,
		int	level )

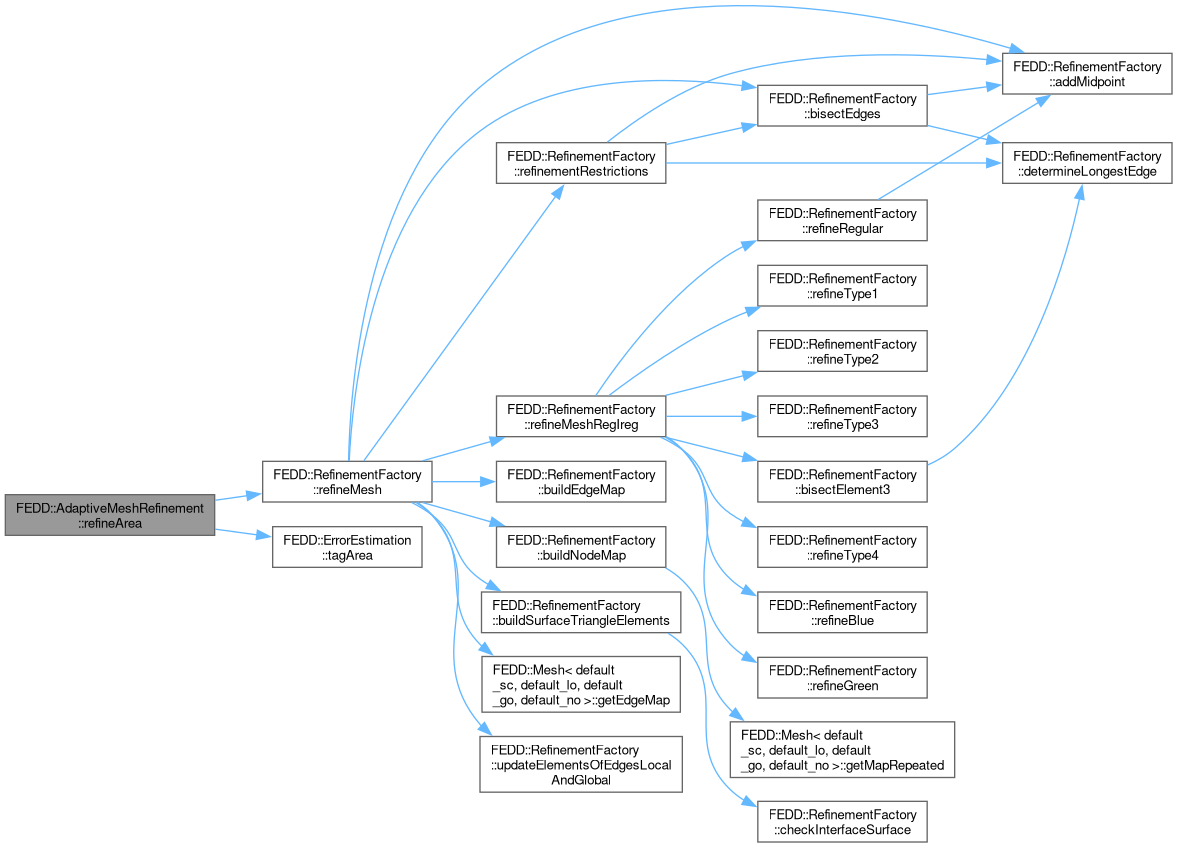
Initializing problem if only a certain area should be refined.

Parameters

[in]	domainP1	P_1 Domain
[in]	area	Area that is suppose to be refined. If is a vector defining the area as follows: row1:[x_0,x_1] x-limits, row2: [y_0,y_1] y-limits, row3: [z_0,z_1] z-limits.
[in]	level	intensity of refinement. Number of levels equals number of performed refinements.

Here is the call graph for this function:

◆ refineUniform()

template<class SC, class LO, class GO, class NO>

AdaptiveMeshRefinement< SC, LO, GO, NO >::DomainPtr_Type FEDD::AdaptiveMeshRefinement< SC, LO, GO, NO >::refineUniform	(	DomainPtr_Type	domainP1,
		int	level )

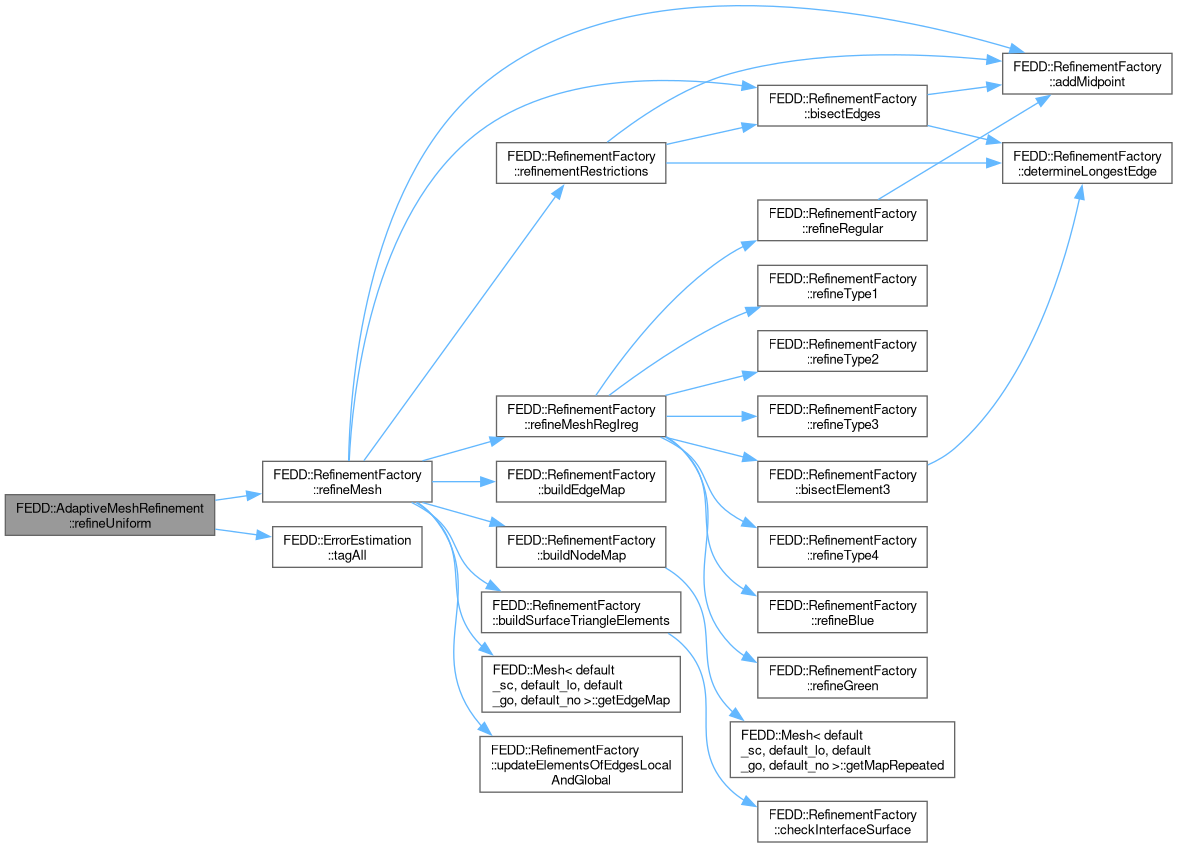
Initializing problem if uniform refinement is requested.

Parameters

[in]	domainP1	P_1 Domain
[in]	level	intensity of refinement. Number of levels equals number of performed refinements.

Here is the call graph for this function:

The documentation for this class was generated from the following files:

feddlib/amr/AdaptiveMeshRefinement_decl.hpp
feddlib/amr/AdaptiveMeshRefinement_def.hpp

Public Types

Public Member Functions

Constructor & Destructor Documentation

◆ AdaptiveMeshRefinement() [1/4]

◆ AdaptiveMeshRefinement() [2/4]

◆ AdaptiveMeshRefinement() [3/4]

◆ AdaptiveMeshRefinement() [4/4]

Member Function Documentation

◆ calcErrorNorms()

◆ exportError()

◆ exportSolution()

◆ globalAlgorithm()

◆ identifyProblem()

◆ refineArea()

◆ refineUniform()