Public Types
typedef Teuchos::RCP< MeshUnstructured< SC, LO, GO, NO > >	MeshUnstrPtr_Type

typedef Elements	Elements_Type

typedef Teuchos::RCP< Elements_Type >	ElementsPtr_Type

typedef EdgeElements	EdgeElements_Type

typedef Teuchos::RCP< EdgeElements_Type >	EdgeElementsPtr_Type

typedef SurfaceElements	SurfaceElements_Type

typedef Teuchos::RCP< SurfaceElements_Type >	SurfaceElementsPtr_Type

typedef Map< LO, GO, NO >	Map_Type

typedef Map_Type::MapPtr_Type	MapPtr_Type

typedef Map_Type::MapConstPtr_Type	MapConstPtr_Type

typedef MultiVector< SC, LO, GO, NO >	MultiVector_Type

typedef Teuchos::RCP< MultiVector_Type >	MultiVectorPtr_Type

typedef MultiVector< LO, LO, GO, NO >	MultiVectorLO_Type

typedef Teuchos::RCP< MultiVectorLO_Type >	MultiVectorLOPtr_Type

typedef Teuchos::RCP< const MultiVector_Type >	MultiVectorConstPtr_Type

typedef Teuchos::OrdinalTraits< LO >	OTLO

typedef Matrix< SC, LO, GO, NO >	Matrix_Type

typedef Teuchos::RCP< Matrix_Type >	MatrixPtr_Type

typedef BlockMultiVector< SC, LO, GO, NO >	BlockMultiVector_Type

typedef Teuchos::RCP< BlockMultiVector_Type >	BlockMultiVectorPtr_Type

typedef Teuchos::RCP< const BlockMultiVector_Type >	BlockMultiVectorConstPtr_Type

Public Member Functions
	ErrorEstimation (int dim, std::string problemType, bool writeMeshQuality_)
	ErrorEstimation is initiated with the dimension and problemType, as it is necessary to fit errorEstimation to the problem at hand.

MultiVectorPtr_Type	estimateError (MeshUnstrPtr_Type inputMeshP12, MeshUnstrPtr_Type inputMeshP1, BlockMultiVectorConstPtr_Type valuesSolution, RhsFunc_Type rhsFunc, std::string FEType)
	Main Function for a posteriori error estimation.

void	identifyProblem (BlockMultiVectorConstPtr_Type valuesSolution)
	Identifying the problem with respect to the degrees of freedom and whether we calculate pressure. By telling how many block the MultiVector has, we can tell whether we calculate pressure or not. Depending on the numbers of entries within the solution vector, we can tell how many degreesOfFreedom (dofs) we have.

void	makeRepeatedSolution (BlockMultiVectorConstPtr_Type valuesSolution)
	We split the solution from the BlockMultiVector valuesSolution into one or more seperate blocks, where the blocks represent the different dimensions.

vec3D_dbl_Type	calcNPhi (std::string phiDerivative, int dofsSol, std::string FEType)
	Function that calculates the jump part for nabla u or p.

vec_dbl_Type	calculateJump ()
	Part of the error estimator that calculates the jump part of the estimation. What kind of jump is calculated depends on the problemType we have at hand.

vec2D_dbl_Type	gradPhi (int dim, int intFE, vec_dbl_Type &p)
	Calcutlating the gradient of phi depending on quad points p.

vec_dbl_Type	phi (int dim, int intFE, vec_dbl_Type &p)
	Calcutlating phi depending on quad points p.

MultiVectorPtr_Type	determineCoarseningError (MeshUnstrPtr_Type mesh_k, MeshUnstrPtr_Type mesh_k_m, MultiVectorPtr_Type errorElementMv_k, std::string distribution, std::string markingStrategy, double theta)
	DetermineCoarseningError is the essential part of the mesh coarsening process.

double	determineResElement (FiniteElement element, RhsFunc_Type rhsFunc)
	Function that that determines \|\|\Delta u_h + f \|\|_(L2(T)), \|\| \Delta u_h + f - \nabla p_h \|\|_T or \|\| \Delta u_h + f - \nabla p_h - (u_h \cdot \nabla)u_h\|\|_T for an Element T.

double	determineDivU (FiniteElement element)
	Function that that determines \|\| div(u) \|\|_T for a Element T.

vec2D_dbl_Type	getQuadValues (int dim, std::string FEType, std::string Type, vec_dbl_Type &QuadW, FiniteElement surface)
	Returns neccesary quadrature Values. Is distinguishes between needing Element or Surface information.

void	markElements (MultiVectorPtr_Type errorElementMv, double theta, std::string strategy, MeshUnstrPtr_Type meshUnstr)
	Function that marks the elements for refinement.

vec_dbl_Type	determineVolTet (ElementsPtr_Type elements, vec2D_dbl_ptr_Type points)
	function, that determines volume of tetrahedra.

vec_dbl_Type	calcDiamTriangles (ElementsPtr_Type elements, vec2D_dbl_ptr_Type points, vec_dbl_Type &areaTriangles, vec_dbl_Type &rho_T, vec_dbl_Type &C_T)
	Calculating the diameter of triangles.

vec_dbl_Type	calcDiamTriangles3D (SurfaceElementsPtr_Type surfaceTriangleElements, vec2D_dbl_ptr_Type points, vec_dbl_Type &areaTriangles, vec_dbl_Type &rho_T, vec_dbl_Type &C_T)
	Calculating the diameter of triangles.

vec_dbl_Type	calcDiamTetraeder (ElementsPtr_Type elements, vec2D_dbl_ptr_Type points, vec_dbl_Type volTet)
	Calculating the circumdiameter of tetraeder.

vec_dbl_Type	calcRhoTetraeder (ElementsPtr_Type elements, SurfaceElementsPtr_Type surfaceTriangleElements, vec_dbl_Type volTet, vec_dbl_Type areaTriangles)
	Calcutlating the incircumdiameter of tetrahedra.

vec_dbl_Type	determineAreaTriangles (ElementsPtr_Type elements, EdgeElementsPtr_Type edgeElements, SurfaceElementsPtr_Type surfaceElements, vec2D_dbl_ptr_Type points)
	Calculating the area of the triangle elements of tetrahedra.

void	buildTriangleMap ()
	Build Surface Map. Contrary to building the edge map, building the surface map is somewhat simpler as elementsOfSurfaceGlobal and elementsOfSurfaceLocal already exist. Via elementsOfSurface global each surface can be uniquely determined by the two elements it connects.

void	updateElementsOfSurfaceLocalAndGlobal (EdgeElementsPtr_Type edgeElements, SurfaceElementsPtr_Type surfaceTriangleElements)
	UpdateElementsOfSurfaceLocalAndGlobal is performed here instead of in meshRefinement, as the information is only needed in case of error estimation. Equivalent function as updateElementsOfEdgeGlobal but with the important destinction, that it runs without communication and only relies on local information.

void	setErrorEstimate (MultiVectorPtr_Type errorElements)

MultiVectorPtr_Type	getErrorEstimate ()

void	tagArea (MeshUnstrPtr_Type meshUnstr, vec2D_dbl_Type area)
	Tags only a certain Area for refinement and is independent of any error estimation.

void	tagAll (MeshUnstrPtr_Type meshUnstr)
	Tags only a certain Area for refinement and is independent of any error estimation.

void	tagFlag (MeshUnstrPtr_Type inputMeshP1, int flag)

Public Attributes
std::string	refinementRestriction_ = "none"

std::string	markingStrategy_ = "Maximum"

double	theta_ = 0.5

bool	writeMeshQuality_ = "false"

bool	timeTablePrint_ = "false"

int	refinement3DDiagonal_ = 0

int	dim_

std::string	problemType_

Protected Attributes
MultiVectorPtr_Type	errorEstimation_

MapConstPtr_Type	surfaceTriangleMap_

SurfaceElementsPtr_Type	surfaceElements_

int	dofs_

int	dofsP_

bool	calculatePressure_ = false

BlockMultiVectorConstPtr_Type	valuesSolutionRepVel_

BlockMultiVectorConstPtr_Type	valuesSolutionRepPre_

Constructor & Destructor Documentation

◆ ErrorEstimation()

template<class SC, class LO, class GO, class NO>

FEDD::ErrorEstimation< SC, LO, GO, NO >::ErrorEstimation	(	int	dim,
		std::string	problemType,
		bool	writeMeshQuality )

ErrorEstimation is initiated with the dimension and problemType, as it is necessary to fit errorEstimation to the problem at hand.

Parameters

[in]	dim	Dimension of problem.
[in]	problemType	Type of problem. Choose between Laplace, Stokes and NavierStokes

Member Function Documentation

◆ buildTriangleMap()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::buildTriangleMap ( )

Build Surface Map. Contrary to building the edge map, building the surface map is somewhat simpler as elementsOfSurfaceGlobal and elementsOfSurfaceLocal already exist. Via elementsOfSurface global each surface can be uniquely determined by the two elements it connects.

The surfacemap is only used for error estimation. Thus it is only build here and not in the refinementFactory.

Here is the caller graph for this function:

◆ calcDiamTetraeder()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::calcDiamTetraeder	(	ElementsPtr_Type	elements,
		vec2D_dbl_ptr_Type	points,
		vec_dbl_Type	volTet )

Calculating the circumdiameter of tetraeder.

Parameters

[in]	elements	Elements.
[in]	points	Points.
[in]	volTet	Volume of tetrahedra.
[out]	diamElements	Uncircumdiameter of tetrahedra.

Here is the caller graph for this function:

◆ calcDiamTriangles()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::calcDiamTriangles	(	ElementsPtr_Type	elements,
		vec2D_dbl_ptr_Type	points,
		vec_dbl_Type &	areaTriangles,
		vec_dbl_Type &	rho_T,
		vec_dbl_Type &	C_T )

Calculating the diameter of triangles.

Parameters

[in]	elements	Elements
[in]	points	Points
[out]	diamElements	Diameter of triangles (Uncirclediameter).
[out]	rho_T	Incirclediameter.
[out]	C_T	Shape parameter.

Here is the caller graph for this function:

◆ calcDiamTriangles3D()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::calcDiamTriangles3D	(	SurfaceElementsPtr_Type	surfaceTriangleElements,
		vec2D_dbl_ptr_Type	points,
		vec_dbl_Type &	areaTriangles,
		vec_dbl_Type &	rho_T,
		vec_dbl_Type &	C_T )

Calculating the diameter of triangles.

Parameters

[in]	elements	Elements.
[in]	points	Points.
[out]	diamElements	Diameter of triangles.

Here is the caller graph for this function:

◆ calcNPhi()

template<class SC, class LO, class GO, class NO>

vec3D_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::calcNPhi	(	std::string	phiDerivative,
		int	dofsSol,
		std::string	FEType )

Function that calculates the jump part for nabla u or p.

Parameters

[in]	phiDerivative	phiDerivative is either 'Gradient' or 'None' and what kind of jump is calculated depends on the problemType we have at hand. If phiDerivative is 'Gradient' the nabla u jump part is caluculated and if its 'None' then the pressure jump.
[in]	dofsSol	Degree of freedom of the caluclated jump part. The pressure dof is always 1 whereas velocity dof can vary depending on the problem.
[in]	FEType	Finite element type of the calculated jump part.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ calcRhoTetraeder()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::calcRhoTetraeder	(	ElementsPtr_Type	elements,
		SurfaceElementsPtr_Type	surfaceTriangleElements,
		vec_dbl_Type	volTet,
		vec_dbl_Type	areaTriangles )

Calcutlating the incircumdiameter of tetrahedra.

Parameters

[in]	elements	Elements.
[in]	surfaceTriangleElements	TriangleElements.
[in]	volTet	Volume of tetrahedra.
[in]	areaTriangles	Area of faces of tetrahedra.
[out]	rhoElements	Incircumdiameter of tetrahedra.

Here is the caller graph for this function:

◆ determineAreaTriangles()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::determineAreaTriangles	(	ElementsPtr_Type	elements,
		EdgeElementsPtr_Type	edgeElements,
		SurfaceElementsPtr_Type	surfaceElements,
		vec2D_dbl_ptr_Type	points )

Calculating the area of the triangle elements of tetrahedra.

Parameters

[in]	elements	Elements.
[in]	edgeElements	Edges.
[in]	surfaceElements	Triangle Elements.
[in]	points	Points.
[out]	areaTriangles	Area of triangles.

◆ determineCoarseningError()

template<class SC, class LO, class GO, class NO>

ErrorEstimation< SC, LO, GO, NO >::MultiVectorPtr_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::determineCoarseningError	(	MeshUnstrPtr_Type	mesh_k,
		MeshUnstrPtr_Type	mesh_k_m,
		MultiVectorPtr_Type	errorElementMv_k,
		std::string	distribution,
		std::string	markingStrategy,
		double	theta )

DetermineCoarseningError is the essential part of the mesh coarsening process.

Instead of calulating an error for mesh level k, we redestribute it to lower mesh levels and refining those. We execute this function with an estimated error from level k. With this calculated error, we mark the elements according to that error and refine afterwards. If we decide to coarsen a certain mesh level, we take that level, look at the k-m level and refine that to the point where we are at the same level we wanted to perform the coarsening on.

Parameters

[in]	mesh_k	Current mesh of level k.
[in]	mesh_k_m	Mesh of refinement level k-m.
[in]	errorElementMv_k	The error estimation of mesh level k.
[in]	distribution	Either 'forwards' or 'backwards'. We determine the error estimate in level k-m with redistributing backwards. if we are in level k-m we calculate the k-m+1 mesh level error estimation via redistributing the k-m error forward.
[in]	markingStrategy	The strategy with which element are marked.
[in]	theta	Marking threshold.

Here is the caller graph for this function:

◆ determineDivU()

template<class SC, class LO, class GO, class NO>

double FEDD::ErrorEstimation< SC, LO, GO, NO >::determineDivU ( FiniteElement element )

Function that that determines || div(u) ||_T for a Element T.

Parameters

[in]	element	FiniteElement element where \|\|div(u)\|\|_T is calculated on.
[out]	divElement	Divergence of u_h on element

Here is the call graph for this function:

Here is the caller graph for this function:

◆ determineResElement()

template<class SC, class LO, class GO, class NO>

double FEDD::ErrorEstimation< SC, LO, GO, NO >::determineResElement	(	FiniteElement	element,
		RhsFunc_Type	rhsFunc )

Function that that determines ||\Delta u_h + f ||_(L2(T)), || \Delta u_h + f - \nabla p_h ||_T or || \Delta u_h + f - \nabla p_h - (u_h \cdot \nabla)u_h||_T for an Element T.

Parameters

[in]	element	FiniteElement element where \|\|div(u)\|\|_T is calculated on.
[in]	rhsFunc	The right hand side function of the pde.
[out]	resElement	Residual of element according to problemType

Here is the call graph for this function:

Here is the caller graph for this function:

◆ determineVolTet()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::determineVolTet	(	ElementsPtr_Type	elements,
		vec2D_dbl_ptr_Type	points )

function, that determines volume of tetrahedra.

Parameters

[in]	elements	Elements.
[in]	edgeElements	Edges.
[in]	points	Points.
[out]	volumeTetrahedra	Volume of tetrahedras

Here is the caller graph for this function:

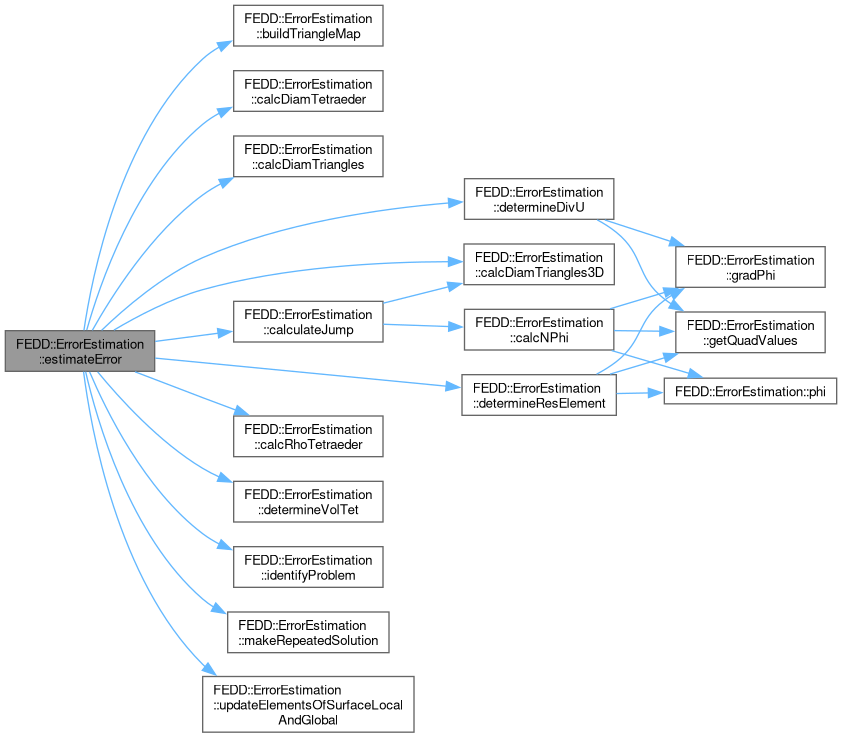
◆ estimateError()

template<class SC, class LO, class GO, class NO>

ErrorEstimation< SC, LO, GO, NO >::MultiVectorPtr_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::estimateError	(	MeshUnstrPtr_Type	inputMeshP12,
		MeshUnstrPtr_Type	inputMeshP1,
		BlockMultiVectorConstPtr_Type	valuesSolution,
		RhsFunc_Type	rhsFunc,
		std::string	FETypeV )

Main Function for a posteriori error estimation.

depending on the problem the the error estimation is calculated accordingly.

Parameters

[in]	inputMeshP1	The P1 Mesh that is used for later refinement.
[in]	inputMeshP12	The possible P2 Mesh, if one of the solutions is of P2 Discretisation, otherwise both meshes are P1.
[in]	solution	Solution of the PDE in BlockMultiVector Format (Block 0: Velocity, Block 1: Pressure).
[in]	rhs	The right hand side function of the pde.
[in]	FETypeV	Finite element type as the maximum FEType for the Velocity, pressure is assumed to be P1 always.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getQuadValues()

template<class SC, class LO, class GO, class NO>

vec2D_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::getQuadValues	(	int	dim,
		std::string	FEType,
		std::string	Type,
		vec_dbl_Type &	QuadW,
		FiniteElement	surface )

Returns neccesary quadrature Values. Is distinguishes between needing Element or Surface information.

Parameters

[in]	dim	Dimension for which the quadrature points are needed.
[in]	FEType	Finite element type for which the quadrature points are needed.
[in]	Type	Type of quadrature points are need. Either 'Element' if you integrate over an element or 'Surface' if you need to integrate over a surface (i.e. for calculating the jump)
[in]	QuadW	Vector to be filled with the quadrature weights accordingly
[in]	FiniteElement	surface for which you need the quadrature points in case if 'Surface' type, as it is needed for figuring out the quadrature points
[out]	QuadPts	Quadrature points
[out]	QuadW	Quadrature weights

Keep in mind that elementwise quadPoint are defined on reference element whereas surface quadPoints are defined on the input surface, which is typically not the reference Element.

Here is the caller graph for this function:

◆ gradPhi()

template<class SC, class LO, class GO, class NO>

vec2D_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::gradPhi	(	int	dim,
		int	intFE,
		vec_dbl_Type &	p )

Calcutlating the gradient of phi depending on quad points p.

Parameters

[in]	dim	Dimension.
[in]	intFE	Integer value of discretisation P1 (1) or P2(2).
[in]	p	Quadpoints or other points for which phi is suppose to be evaluated.
[out]	gradPhi	Gradient of phi with evaluated values p.

Here is the caller graph for this function:

◆ identifyProblem()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::identifyProblem ( BlockMultiVectorConstPtr_Type valuesSolution )

Identifying the problem with respect to the degrees of freedom and whether we calculate pressure. By telling how many block the MultiVector has, we can tell whether we calculate pressure or not. Depending on the numbers of entries within the solution vector, we can tell how many degreesOfFreedom (dofs) we have.

Parameters

[in] valuesSolution Blocks that contains solution for velocity and as the case may be pressure.

Here is the caller graph for this function:

◆ makeRepeatedSolution()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::makeRepeatedSolution ( BlockMultiVectorConstPtr_Type valuesSolution )

We split the solution from the BlockMultiVector valuesSolution into one or more seperate blocks, where the blocks represent the different dimensions.

Parameters

[in] valuesSolution Block that contains solution for velocity and as the case may be pressure.

Here is the caller graph for this function:

◆ markElements()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::markElements	(	MultiVectorPtr_Type	errorElementMv,
		double	theta,
		std::string	strategy,
		MeshUnstrPtr_Type	meshP1 )

Function that marks the elements for refinement.

Parameters

[in]	errorElementMv	MultiVector that contains the estimated error for each element.
[in]	theta	Parameter determining for marking strategies.
[in]	markingStrategy	Strategy with which the elements are marked. Implemented Strategies 'Doerfler' or 'Maximum'.
[in]	meshP1	P1 mesh which is used for later refinement and has to be the one beeing marked.

!! it is essential that the meshP1 mesh inserted here is the mesh that will be used for mesh refinement, as it contains the elementwise-information determining refinement. !!

Here is the caller graph for this function:

◆ phi()

template<class SC, class LO, class GO, class NO>

vec_dbl_Type FEDD::ErrorEstimation< SC, LO, GO, NO >::phi	(	int	dim,
		int	intFE,
		vec_dbl_Type &	p )

Calcutlating phi depending on quad points p.

Parameters

[in]	dim.
[in]	intFE	integer value of discretisation P1 (1) or P2(2).
[in]	p	Quadpoints or other points for which phi is to be evaluated.
[out]	phi	Phi with evaluated values p.

Here is the caller graph for this function:

◆ tagAll()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::tagAll ( MeshUnstrPtr_Type inputMeshP1 )

Tags only a certain Area for refinement and is independent of any error estimation.

Parameters

[in]	inputMeshP1	The P1 Mesh that is used for later refinement.
[in]	area	Area that is suppose to be refined. If is a vector defining the area as follows: row1:[x_0,x_1] x-limits, row2: [y_0,y_1] y-limits, row3: [z_0,z_1] z-limits .

Here is the caller graph for this function:

◆ tagArea()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::tagArea	(	MeshUnstrPtr_Type	inputMeshP1,
		vec2D_dbl_Type	area )

Tags only a certain Area for refinement and is independent of any error estimation.

Parameters

[in]	inputMeshP1	The P1 Mesh that is used for later refinement.
[in]	area	Area that is suppose to be refined. If is a vector defining the area as follows: row1:[x_0,x_1] x-limits, row2: [y_0,y_1] y-limits, row3: [z_0,z_1] z-limits .

Here is the caller graph for this function:

◆ updateElementsOfSurfaceLocalAndGlobal()

template<class SC, class LO, class GO, class NO>

void FEDD::ErrorEstimation< SC, LO, GO, NO >::updateElementsOfSurfaceLocalAndGlobal	(	EdgeElementsPtr_Type	edgeElements,
		SurfaceElementsPtr_Type	surfaceTriangleElements )

UpdateElementsOfSurfaceLocalAndGlobal is performed here instead of in meshRefinement, as the information is only needed in case of error estimation. Equivalent function as updateElementsOfEdgeGlobal but with the important destinction, that it runs without communication and only relies on local information.

Parameters

[in]	edgeElements	Edes.
[in]	surfaceTriangleElements	Triangle elements.

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

feddlib/amr/ErrorEstimation_decl.hpp
feddlib/amr/ErrorEstimation_def.hpp

Public Types

Public Member Functions

Public Attributes

Protected Attributes

Constructor & Destructor Documentation

◆ ErrorEstimation()

Member Function Documentation

◆ buildTriangleMap()

◆ calcDiamTetraeder()

◆ calcDiamTriangles()

◆ calcDiamTriangles3D()

◆ calcNPhi()

◆ calcRhoTetraeder()

◆ determineAreaTriangles()

◆ determineCoarseningError()

◆ determineDivU()

◆ determineResElement()

◆ determineVolTet()

◆ estimateError()

◆ getQuadValues()

◆ gradPhi()

◆ identifyProblem()

◆ makeRepeatedSolution()

◆ markElements()

◆ phi()

◆ tagAll()

◆ tagArea()

◆ updateElementsOfSurfaceLocalAndGlobal()